Ada yang pernah dengar Tensor? Tensor bukanlah singkatan dari transformasi sensor atau tentang sensor ortogonal. Kalau mau mengerti, Mari Kita belajar sedikit demi sedikit tentang Tensor.
Tensor merupakan bagian dari analisis matematik suatu bentuk representasi yang lebih umum.
Definisi sebuah vektor dapat diperluas untuk mendefinisikan jenis yang lebih umum
sebuah objek yang dinamakan tensor, yang bisa memiliki subscript lebih dari satu.
Skalar, vektor, dan matriks harus bisa bertransformasi secara ortogonal supaya dapat dikatakan tensor.
Jika dalam sistem koordinat persegi ruang tiga dimensi dibawah rotasi koordinat:
kuantitas 3N Ti1,i2,···,iN
(dengan tiap i1,i2,··· ,iN merupakan indeks bebas berjalan dari 1 ke 3) bertransformasi menurut aturan
sehingga Ti1,i2,···,iN adalah komponen dari tensor Cartesian rank N.
Rank sebuah tensor adalah jumlah subscript bebas. Sehingga tensor dengan rank nol
hanya memiliki satu buah komponen (3^0 = 1). Sehingga kita bisa menganggapnya
sebagai skalar.
Tensor dengan rank satu memiliki tiga buah komponen (3^1 = 3). Aturan transformasi
komponen-komponennya di bawah rotasi sama dengan aturan pada vektor. Sehingga
vektor adalah tensor rank satu.
Kasus lainnya paling penting adalah tensor rank dua. Tensor ini memiliki sembilan
buah komponen (3^2 = 9), Tij mengikuti aturan transformasi
Komponen-komponen tensor rank dua dapat dinyatakan dalam matriks 3×3:
Tetapi, hal ini tidak berarti tiap matriks 3 × 3 membentuk sebuah tensor. Syarat paling
penting adalah komponen-komponennya memenuhi aturan transformasi.
Sebagai masalah terminologi, tensor rank dua dalam ruang tiga dimensi memiliki
sembilan buah komponen Tij. Tetapi sering Tij dianggap sebagai “tensor” dibandingkan
“komponen tensor” untuk sederhananya. Dengan kata lain, Tij digunakan untuk
menyatakan komponen keseluruhan sekaligus komponen individu.
Tensor banyak digunakan dalam fisika seperti:
# Materi:
o Elektron bebas
o Medan isotropik
o Medan anisotropik: Elastisitas, Kelistrikan, Magnetik
# Teori Elektromagnetik
# Relativitas Contoh Soal:
Tunjukkan bahwa dalam ruang dua dimensi, kuantitas berikut merupakan tensor rank
dua
>> Penyelesaian:
Dalam ruang dua dimensi, tensor rank dua memiliki 4 (2^2 = 4) komponen. Jika ini adalah tensor maka dalam koordinat terotasi bentuknya haruslah
dengan
sekarang kita
harus memeriksa jika tiap komponen memenuhi aturan transformasi
Hal ini harus
dibandingkan dengan
Terlihat bahwa dua buah ekspresi identik. Proses
yang sama akan menunjukkan bahwa komponen-komponen lain juga memenuhi aturan
transformasi. Sehingga Tij adalah tensor rank dua dalam ruang dua
dimensi.
Referensi:
K. T. Tang. Diktat Fisika Matematika II, Universitas Islam Negeri Sunan Gunung Djati. Tidak diterbitkan.








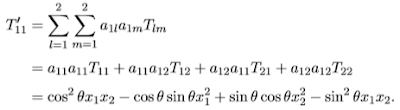



Tidak ada komentar:
Posting Komentar